

Two-dimensional rigid bodies have only one degree of rotational freedom, so they can be solved using just one moment equilibrium equation, but to solve three-dimensional rigid bodies, which have six degrees of freedom, all three moment equations and all three force equations are required. To analyze rigid bodies, which can rotate as well as translate, the moment equations are needed to address the additional degrees of freedom. We saw in Chapter 3 that particle equilibrium problems can be solved using the force equilibrium equation alone, because particles have, at most, three degrees of freedom and are not subject to any rotation. Figure 3.5: Stress gradient in a solid half-space and derivation of total vertical stress as a function of depth. Integration of the third equation yields the (vertical) stress, ( 3. The only equation we can solve is the third one. In many cases we do not need all six equations. Notice there are 6 unknowns and 3 equations in Eq. The stress components on each side of the cube is a function of the position since we have a non uniform but continuous stress field.Working with these scalar equations is often easier than using their vector equivalents, particularly in two-dimensional problems. The stress resultant on A is thus determined on the basis of known stresses s x, s y, s z, t xy, t xz and t yz and a knowledge of. These equations give 6 independent equations in 3D space for each (rigid) body. (a), we obtain, after canceling A, Equation 1.26. A (rigid) body is said to in equilibrium if the vector sum of ALL forces. Next, from the equilibrium of x, y, z-directed forces together with Eq. The stresses acting on the opposite sides of the cube are slightly different. When the coefcients of i, j, and k in the resulting moment equation are set equal to zero, respectively, we obtain the three scalar moment equations Mx 0. Here i, j, and k are unit vectors in the x, y, and z directions, respectively. Figure 1: Infinitesimal parallelepiped representing a point in a body under static equilibrium. We will assume that the stress field is continuous and differentiable inside the whole body. We cut an infinitesimal parallelepiped inside the body and we analyze the forces that act on it as shown in Fig. Surface and body forces act on this body. This approach may be found in international bibliography.Ĭonsider a solid body in static equilibrium that neither moves nor rotates.

A more elegant solution may be derived by using Gauss's theorem and Cauchy's formula. In this article we will prove the equilibrium equations by calculating the resultant force and moment on each axis. This can be expressed by the equilibrium equations. There are six equations expressing the equilibrium of a rigid body in 3 dimensions. The algorithm first solves the equilibrium force balance equation for the current density J.
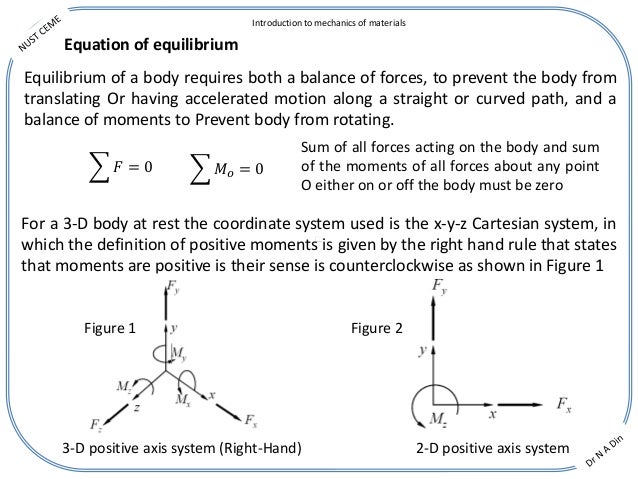
At this point, your work involves algebra only. Keep in mind that the number of equations must be the same as the number of unknowns. These are F X F Y F Z 0 M X M Y M Z 0 The moment equations can be determined about any point. These two vector equations can be written as six scalar equations of equilibrium (EofE). If the number of unknowns is larger than the number of equations, the problem cannot be solved. As stated earlier, when a body is in equilibrium, the net force and the net moment equal zero, i.e., F 0 and M O 0.
#EQUATIONS OF EQUILIBRIUM 3D PLUS#
17, 2020Ī solid body is in static equilibrium when the resultant force and moment on each axis is equal to zero. including a 3D stellarator equilibrium at 2. EQUILIBRIUM 3D PLUS Evaluate the expressions for the unknown quantities that you obtained in your solution. Get access to the latest Equation of Equilibrium 3D prepared with GATE & ESE course curated by Shahnawaz Mohd on Unacademy to prepare for the toughest.


 0 kommentar(er)
0 kommentar(er)
